Chapter 4
Solving the Schrödinger equation
p. 95 - Intro
p. 96 - Section 4.1
p. 98 - Section 4.2
p. 102 - Section 4.3
p. 111 - Section 4.4
p. 132 - Section 4.5
Determine whether each of the following functions meets the requirements of a quantum wavefunction:
(a) \(f(x)=\frac{1}{(x-x_0)^2}\) over the range \(x=-\infty\) to \(+\infty\).
(b) \(g(x)=\sin{(kx)}\) over the range \(x=-\pi\) to \(\pi\) (\(k\) is finite).
(c) \(h(x)=\sin^{-1}{(x)}\) over the range \(x=-1\) to \(1\).
(d) \(\psi(x)=Ae^{ikx}\) (constant \(A\)) over the range \(x=-\infty\) to \(+\infty\).
As described in Section 4.3, to qualify as a quantum wavefunction, a function must not only satisfy the Schrödinger equation and fit the boundary conditions, it must also be single-valued, smooth, and square-integrable. Since the function \(f(x)=\frac{1}{(x-x_0)^2}\) becomes infinitely large at the location \(x=x_0\), it does not meet the requirement for square-integrability (unlike the delta function, which is infinitely large at one location but is also infinitely narrow).
This sine function is single-valued and smooth, and since it is limited to the region \(kx=-1\) to \(1\) radian, it is also square-integrable. It therefore meets these requirements for a quantum wavefunction.
Since the arcsin is multivalued (that is, there are multiple values of \(\sin^{-1}(x)\) for a single value of \(x\)), it does not satisfy the requirement that quantum wavefunctions must be single-valued.
Since the complex-exponential function for a single wavenumber \(k\) has infinite spatial extent and is not square-integrable, this function does not meet the requirements for a quantum wavefunction (but, as mentioned in the discussion of square-integrability in the text, it is possible to form combinations of these functions (“wave packets”) that have limited spatial extent and are square-integrable).
As described in Section 4.3, to qualify as a quantum wavefunction, a function must not only satisfy the Schrödinger equation and fit the boundary conditions, it must also be single-valued, smooth, and square-integrable.
For Part (a), since the function \(f(x)=\frac{1}{(x-x_0)^2}\) becomes infinitely large at the location \(x=x_0\), it does not meet the requirement for square-integrability (unlike the delta function, which is infinitely large at one location but is also infinitely narrow).
For Part (b), this sine function is single-valued and smooth, and since it is limited to the region \(kx=-1\) to \(1\) radian, it is also square-integrable. It therefore meets these requirements for a quantum wavefunction.
For Part (c), since the arcsin is multivalued (that is, there are multiple values of \(\sin^{-1}(x)\) for a single value of \(x\)), it does not satisfy the requirement that quantum wavefunctions must be single-valued.
For Part (d), since the complex-exponential function for a single wavenumber \(k\) has infinite spatial extent and is not square-integrable, this function does not meet the requirements for a quantum wavefunction (but, as mentioned in the discussion of square-integrability in the text, it is possible to form combinations of these functions (“wave packets”) that have limited spatial extent and are square-integrable).
Use the sifting property of the Dirac delta function to evaluate these integrals:
(a) \(\int_{-\infty}^{\infty}Ax^2e^{ikx}\delta (x-x_0)dx\).
(b) \(\int_{-\infty}^{\infty}\cos{(kx)}\delta (k’-k)dk\).
(c) \(\int_{-2}^{3}\sqrt{x}\delta (x+3)dx\).
As described in Section 4.4, the Dirac delta function inside an integral may perform a “sifting” function illustrated by Eq. 4.31:
\begin{equation*}
\int_{-\infty}^\infty f(x’)\delta(x’-x)dx’=f(x).
\end{equation*}
as long as the argument of the delta function (\(x’-x_0\) in this case) equals zero within the limits of integration.
The argument of \(\delta (x-x_0)\) is zero at the location \(x=x_0\), which is within the limits of integration (which are \(-\infty\) to \(+\infty\) in this case). Thus the integrand is non-zero only at \(x=x_0\), and the function evaluated at that location comes out of the integral:
\begin{equation*}
\int_{-\infty}^{\infty}Ax^2e^{ikx}\delta (x-x_0)dx=Ax^2e^{ikx_0}.
\end{equation*}
In this case, the argument of \(\delta (k’-k)\) is zero at the location \(k=k’\), which is within the limits of integration (\(-\infty\) to\(+\infty\)). Thus the integrand is non-zero only at \(k=k’\), and the function evaluated at that location comes out of the integral:
\begin{equation*}
\int_{-\infty}^{\infty}\cos{(kx)}\delta (k’-k)dk=\cos{(k’x)}.
\end{equation*}
The argument of the delta function \(\delta (x+3)\) is zero at the location \(x=-3\), but that location is not within the limits of integration (which are \(-2\) to \(+3\) in this case). Thus the integrand is zero over the entire range of integration:
\begin{equation*}
\int_{-2}^{3}\sqrt{x}\delta (x+3)dx=0.
\end{equation*}
As described in Section 4.4, the Dirac delta function inside an integral may perform a “sifting” function illustrated by Eq. 4.31:
\begin{equation*}
\int_{-\infty}^\infty f(x’)\delta(x’-x)dx’=f(x).
\end{equation*}
as long as the argument of the delta function (\(x’-x_0\) in this case) equals zero within the limits of integration.
For Part (a), the argument of \(\delta (x-x_0)\) is zero at the location \(x=x_0\), which is within the limits of integration (which are \(-\infty\) to \(+\infty\) in this case). Thus the integrand is non-zero only at \(x=x_0\), and the function evaluated at that location comes out of the integral:
\begin{equation*}
\int_{-\infty}^{\infty}Ax^2e^{ikx}\delta (x-x_0)dx=Ax^2e^{ikx_0}.
\end{equation*}
For Part (b), the argument of \(\delta (k’-k)\) is zero at the location \(k=k’\), which is within the limits of integration \((-\infty\) to\(+\infty\)). Thus the integrand is non-zero only at \(k=k’\), and the function evaluated at that location comes out of the integral:
\begin{equation*}
\int_{-\infty}^{\infty}\cos{(kx)}\delta (k’-k)dk=\cos{(k’x)}.
\end{equation*}
For Part (c), the argument of the delta function \(\delta (x+3)\) is zero at the location \(x=-3\), but that location is not within the limits of integration (which are \(-2\) to \(+3\) in this case). Thus the integrand is zero over the entire range of integration:
\begin{equation*}
\int_{-2}^{3}\sqrt{x}\delta (x+3)dx=0.
\end{equation*}
Show that the Fourier-transform relationships between the position-space and momentum-space representations of the state represented by ket \(\ket{\psi}\) (Eqs. 4.38 and 4.39) can be written as
\begin{equation*}
\tilde{\phi}(p)=\braket{p\vert\psi}=\int_{-\infty}^{\infty} \braket{p\vert x}\braket{x\vert\psi}dx
\end{equation*}
and
\begin{equation*}
\psi(x)=\braket{x\vert\psi}=\int_{-\infty}^{\infty} \braket{x\vert p}\braket{p\vert\psi} dp\\
\end{equation*}
if the momentum and position basis vectors are defined such that \(\braket{p\vert x}=e^{-i\frac{p}{\hbar}x}/\sqrt{2\pi}\).
The Fourier-transform relationship of Eq. 4.38 is
\begin{equation*}
\tilde{\phi}(p)=\frac{1}{\sqrt{2\pi}}\int_{-\infty}^\infty \psi(x)e^{-i\frac{p}{\hbar}x}dx
\end{equation*}
which can be re-arranged to look like this:
\begin{equation*}
\tilde{\phi}(p)=\int_{-\infty}^\infty \frac{1}{\sqrt{2\pi}} e^{-i\frac{p}{\hbar}x}\psi(x) dx.
\end{equation*}
The problem statement says that \(\frac{1}{\sqrt{2\pi}} e^{-i\frac{p}{\hbar}x}=\braket{p\vert x}\), and you know that the position wavefunction \(\psi(x)\) is given by the projection of \(\psi\) on the position basis vectors, so \(\psi(x)=\braket{x\vert\psi}\).
Inserting the expressions from the previous hint into the Fourier-transform relationship gives
\begin{equation*}
\tilde{\phi}(p)=\int_{-\infty}^\infty \braket{p\vert x}\braket{x\vert\psi} dx.
\end{equation*}
And since \(\ket{x}\bra{x}\) is a projection operator and integrating that operator over all space gives the identity operator, \(\tilde{\phi}(p)\) may be written as
\begin{equation*}
\tilde{\phi}(p)=\braket{p} I \ket{\psi}=\braket{p\vert\psi}.
\end{equation*}
The inverse Fourier-transform relationship of Eq. 4.39 is
\begin{equation*}
\psi(x)=\frac{1}{\sqrt{2\pi}}\int_{-\infty}^\infty \tilde{\phi}(p)e^{i\frac{p}{\hbar}x}dp
\end{equation*}
which can be re-arranged to look like this:
\begin{equation*}
\psi(x)=\int_{-\infty}^\infty \frac{1}{\sqrt{2\pi}} e^{i\frac{p}{\hbar}x}\tilde{\phi}(p) dp.
\end{equation*}
Recall that reversing the order of the functions in an inner product gives the complex conjugate of the non-reversed case, so \(\frac{1}{\sqrt{2\pi}} e^{i\frac{p}{\hbar}x}=\braket{x\vert p}\). Recall also that \(\tilde{\phi}(p)=\braket{p\vert\psi}\).
Inserting the expressions from the previous hint into the inverse Fourier-transform relationship gives
\begin{equation*}
\psi(x)=\int_{-\infty}^\infty \braket{x\vert p}\braket{p\vert\psi} dp.
\end{equation*}
And since \(\ket{p}\bra{p}\) is a projection operator and integrating that operator over all momentum space gives the identity operator, \(\psi(x)\) may be written as
\begin{equation*}
\psi(x)=\bra{x} I \ket{\psi}=\braket{x\vert\psi}.
\end{equation*}
The Fourier-transform relationship of Eq. 4.38 is
\begin{equation*}
\tilde{\phi}(p)=\frac{1}{\sqrt{2\pi}}\int_{-\infty}^\infty \psi(x)e^{-i\frac{p}{\hbar}x}dx
\end{equation*}
which can be re-arranged to look like this:
\begin{equation*}
\tilde{\phi}(p)=\int_{-\infty}^\infty \frac{1}{\sqrt{2\pi}} e^{-i\frac{p}{\hbar}x}\psi(x) dx.
\end{equation*}
The problem statement says that \(\frac{1}{\sqrt{2\pi}} e^{-i\frac{p}{\hbar}x}=\braket{p\vert x}\), and you know that the position wavefunction \(\psi(x)\) is given by the projection of \(\psi\) on the position basis vectors, so \(\psi(x)=\braket{x\vert\psi}\). Inserting these expressions into the Fourier-transform relationship gives
\begin{equation*}
\tilde{\phi}(p)=\int_{-\infty}^\infty \braket{p\vert x}\braket{x\vert\psi} dx.
\end{equation*}
Since \(\ket{x}\bra{x}\) is a projection operator and integrating that operator over all space gives the identity operator, \(\tilde{\phi}(p)\) may be written as
\begin{equation*}
\tilde{\phi}(p)=\bra{p} I \ket{\psi}=\braket{p\vert\psi}.
\end{equation*}
The inverse Fourier-transform relationship of Eq. 4.39 is
\begin{equation*}
\psi(x)=\frac{1}{\sqrt{2\pi}}\int_{-\infty}^\infty \tilde{\phi}(p)e^{i\frac{p}{\hbar}x}dp,
\end{equation*}
which can be re-arranged to look like this:
\begin{equation*}
\psi(x)=\int_{-\infty}^\infty \frac{1}{\sqrt{2\pi}} e^{i\frac{p}{\hbar}x}\tilde{\phi}(p) dp.
\end{equation*}
Recall that reversing the order of the functions in an inner product gives the complex conjugate of the non-reversed case, so \(\frac{1}{\sqrt{2\pi}} e^{i\frac{p}{\hbar}x}=\braket{x\vert p}\). Recall also that \(\tilde{\phi}(p)=\braket{p\vert\psi}\), and inserting these expressions into the inverse Fourier-transform relationship gives
\begin{equation*}
\psi(x)=\int_{-\infty}^\infty \braket{x\vert p}\braket{p\vert\psi} dp.
\end{equation*}
Since \(\ket{p}\bra{p}\) is a projection operator and integrating that operator over all momentum space gives the identity operator, \(\psi(x)\) may be written as
\begin{equation*}
\psi(x)=\bra{x} I \ket{\psi}=\braket{x\vert\psi}.
\end{equation*}
Use Eq. 4.53 to find the expectation value \(\braket{x}\) for a particle with position-basis wavefunction \(\psi(x)=\sqrt{\frac{2}{a}}\sin{\left(\frac{2\pi x}{a}\right)}\) over the range \(x=0\) to \(x=a\) and zero elsewhere.
The expectation value of \(x\) is given by Eq. 4.53 as
\begin{equation*}
\braket{x}=\int_{-\infty}^\infty x|\psi(x)|^2dx=\int_{-\infty}^\infty [\psi(x)]^*x[\psi(x)] dx
\end{equation*}
and in this case \(\psi(x)\) exists only over the range of \(x=0\) to \(x=a\). In that range, \(\psi(x)=\sqrt{\frac{2}{a}}\sin{\left(\frac{2\pi x}{a}\right)}\).
Inserting the expression for \(\psi(x)\) into Eq. 4.53 gives
\begin{equation*}
\braket{x}=\int_{0}^a \left[\sqrt{\frac{2}{a}}\sin{\left(\frac{2\pi x}{a}\right)}\right]^*x\left[\sqrt{\frac{2}{a}}\sin{\left(\frac{2\pi x}{a}\right)}\right] dx
\end{equation*}
or
\begin{equation*}
\braket{x}=\int_{0}^a x\left[\sqrt{\frac{2}{a}}\sin{\left(\frac{2\pi x}{a}\right)}\right]^2 dx.
\end{equation*}
The integral
\begin{equation*}
\int_{0}^a x\sin^2{\left(\frac{2\pi x}{a}\right)} dx
\end{equation*}
can be evaluated using
\begin{equation*}
\int x \sin^2{(bx)} dx=\frac{x^2}{4}-\frac{x\sin{(2bx)}}{4b}-\frac{\cos{(2bx)}}{8b^2}.
\end{equation*}
In this case \(b=\frac{2\pi}{a}\), so
\begin{equation*}
\int_0^a x \sin^2{\left(\frac{2\pi}{a}x\right)} dx=\frac{x^2}{4}-\frac{x\sin{\left(\frac{4\pi}{a}x\right)}}{4\left(\frac{2\pi}{a}\right)}-\frac{\cos{(\frac{4\pi}{a}x)}}{8\left(\frac{2\pi}{a}\right)^2}\bigg|_0^a.
\end{equation*}
or
\begin{align*}
\int_0^a x \sin^2{\left(\frac{2\pi}{a}x\right)} dx&=\frac{a^2}{4}-0-\frac{\cos{(\frac{4\pi}{a}a)}}{8\left(\frac{2\pi}{a}\right)^2}+\frac{\cos{(0)}}{8\left(\frac{2\pi}{a}\right)^2}\\
&=\frac{a^2}{4}.
\end{align*}
Multiplying the expression from the previous hint by the constant factor \(\frac{2}{a}\) in front of the integral gives
\begin{equation*}
\braket{x}=\frac{2}{a}\left(\frac{a^2}{4}\right)=\frac{a}{2}.
\end{equation*}
The expectation value of \(x\) is given by Eq. 4.53 as
\begin{equation*}
\braket{x}=\int_{-\infty}^\infty x|\psi(x)|^2dx=\int_{-\infty}^\infty [\psi(x)]^*x[\psi(x)] dx
\end{equation*}
and in this case \(\psi(x)\) exists only over the range of \(x=0\) to \(x=a\). In that range, \(\psi(x)=\sqrt{\frac{2}{a}}\sin{\left(\frac{2\pi x}{a}\right)}\).
Inserting the expression for\(\psi(x)\) into Eq. 4.53 gives
\begin{equation*}
\braket{x}=\int_{0}^a \left[\sqrt{\frac{2}{a}}\sin{\left(\frac{2\pi x}{a}\right)}\right]^*x\left[\sqrt{\frac{2}{a}}\sin{\left(\frac{2\pi x}{a}\right)}\right] dx
\end{equation*}
or
\begin{equation*}
\braket{x}=\int_{0}^a x\left[\sqrt{\frac{2}{a}}\sin{\left(\frac{2\pi x}{a}\right)}\right]^2 dx.
\end{equation*}
The integral
\begin{equation*}
\int_{0}^a x\sin^2{\left(\frac{2\pi x}{a}\right)} dx
\end{equation*}
can be evaluated using
\begin{equation*}
\int x \sin^2{(bx)} dx=\frac{x^2}{4}-\frac{x\sin{(2bx)}}{4b}-\frac{\cos{(2bx)}}{8b^2}.
\end{equation*}
In this case\(b=\frac{2\pi}{a}\), so
\begin{equation*}
\int_0^a x \sin^2{\left(\frac{2\pi}{a}x\right)} dx=\frac{x^2}{4}-\frac{x\sin{\left(\frac{4\pi}{a}x\right)}}{4\left(\frac{2\pi}{a}\right)}-\frac{\cos{(\frac{4\pi}{a}x)}}{8\left(\frac{2\pi}{a}\right)^2}\bigg|_0^a.
\end{equation*}
or
\begin{align*}
\int_0^a x \sin^2{\left(\frac{2\pi}{a}x\right)} dx&=\frac{a^2}{4}-0-\frac{\cos{(\frac{4\pi}{a}a)}}{8\left(\frac{2\pi}{a}\right)^2}+\frac{\cos{(0)}}{8\left(\frac{2\pi}{a}\right)^2}\\
&=\frac{a^2}{4}.
\end{align*}
Multiplying this expression by the constant factor \(\frac{2}{a}\) in front of the integral gives
\begin{equation*}
\braket{x}=\frac{2}{a}\left(\frac{a^2}{4}\right)=\frac{a}{2}.
\end{equation*}
Show that in two regions of piecewise-constant potential the amplitude ratio of the wavefunctions (such as \(\psi(x)\) given by Eq. 4.10) on opposite sides of the boundary between the regions is inversely proportional to the wavenumber ratio (assume \(E>V\) on both sides of the boundary).
As described in Section 4.3, both the wavefunction \(\psi(x)\) and its slope (the first spatial derivative) \(\partial \psi(x)/\partial x\) must be continuous across the boundary.
For the wavefunction with form
\begin{equation*}
\psi(x)=Ae^{ikx}+Be^{-ikx}
\end{equation*}
you can write the wavefunctions \(\psi_1(x)\) on one side of the boundary and \(\psi_2(x)\) on the other side of the boundary as
\begin{equation*}
\psi_1(x)=A_1e^{ik_1x}+B_1e^{-ik_1x}
\end{equation*}
and
\begin{equation*}
\psi_2(x)=A_2e^{ik_2x}+B_2e^{-ik_2x}
\end{equation*}
and their first spatial derivatives as
\begin{align*}
\frac{\partial \psi_1(x)}{\partial x}&=\frac{\partial (A_1e^{ik_1x})}{\partial x}+\frac{\partial (B_1e^{-ik_1x})}{\partial x}\\
&=ik_1A_1e^{ik_1x}-ik_1B_1e^{-ik_1x}
\end{align*}
and
\begin{align*}
\frac{\partial \psi_2(x)}{\partial x}&=\frac{\partial (A_2e^{ik_2x})}{\partial x}+\frac{\partial (B_2e^{-ik_2x})}{\partial x}\\
&=ik_2A_2e^{ik_2x}-ik_2B_2e^{-ik_2x}.
\end{align*}
To use the continuity of the wavefunction \(\psi\) and its derivative across the boundary to find the relationship between wavenumber and amplitude, find the square magnitude of each of the expressions in the previous hint.
The squares of \(\psi\) and its spatial derivative on each side of the boundary are
\begin{align*}
|\psi_1(x)|^2=(\psi_1)(\psi_1)^*&=(A_1e^{ik_1x}+B_1e^{-ik_1x})(A_1e^{ik_1x}+B_1e^{-ik_1x})^*\\
&=A_1^2+B_1^2+A_1B_1\left(e^{2ik_1x}+e^{-2ik_1x}\right)\\
&=A_1^2+B_1^2+2A_1B_1\cos{(2ik_1x)}
\end{align*}
\begin{align*}
|\psi_2(x)|^2=(\psi_2)(\psi_2)^*&=(A_2e^{ik_2x}+B_2e^{-ik_2x})(A_2e^{ik_2x}+B_2e^{-ik_2x})^*\\
&=A_2^2+B_2^2+A_2B_2\left(e^{2ik_2x}+e^{-2ik_2x}\right)\\
&=A_2^2+B_2^2+2A_2B_2\cos{(2ik_2x)}
\end{align*}
\begin{align*}
\bigg|\frac{\partial \psi_1(x)}{\partial x}\bigg|^2&=(ik_1A_1e^{ik_1x}-ik_1B_1e^{-ik_1x})(ik_1A_1e^{ik_1x}-ik_1B_1e^{-ik_1x})^*\\
&=k_1^2\left[A_1^2+B_1^2-A_1B_1\left(e^{2ik_1x}+e^{-2ik_1x}\right)\right]\\
&=k_1^2\left[A_1^2+B_1^2-2A_1B_1\cos{(2ik_1x)}\right]
\end{align*}
\begin{align*}
\bigg|\frac{\partial \psi_2(x)}{\partial x}\bigg|^2&=(ik_2A_2e^{ik_2x}-ik_2B_2e^{-ik_2x})(ik_2A_2e^{ik_2x}-ik_2B_1e^{-ik_2x})^*\\
&=k_2^2\left[A_2^2+B_2^2-A_2B_2\left(e^{2ik_2x}+e^{-2ik_2x}\right)\right]\\
&=k_2^2\left[A_2^2+B_2^2-2A_2B_2\cos{(2ik_2x)}\right].
\end{align*}
In the expressions in the previous hint, the \(A_1^2+B_1^2\) and \(A_2^2+B_2^2\) provide information about the amplitude of the wavefunctions on opposite sides of the boundary, but those pesky \(2A_1B_1\cos{(2ik_1x)}\) and \(2A_2B_2\cos{(2ik_2x)}\) cross terms make it somewhat difficult to see that information.
Notice, however, that the cross terms in \(|\psi|^2\) have the opposite signs of those in \(|\frac{\partial \psi}{\partial x}|^2\). So those cross terms will cancel if you add \(|\psi|^2\) to \(|\frac{\partial \psi}{\partial x}|^2\) (after dividing the latter by the \(k^2\) factor that appears in \(|\frac{\partial \psi}{\partial x}|^2\) but not in \(|\psi|^2\)).
The additions described in the previous hint give
\begin{align*}
|\psi_1(x)|^2+\frac{1}{k_1^2}\bigg|\frac{\partial \psi_1(x)}{\partial x}\bigg|^2&=A_1^2+B_1^2+2A_1B_1\cos{(2ik_1x)}\\
&\hspace{0.25cm}+\left(\frac{1}{k_1^2}\right)k_1^2\left[A_1^2+B_1^2-2A_1B_1\cos{(2ik_1x)}\right]\\
&=2(A_1^2+B_1^2)
\end{align*}
and
\begin{align*}
|\psi_2(x)|^2+\frac{1}{k_2^2}\bigg|\frac{\partial \psi_2(x)}{\partial x}\bigg|^2&=A_2^2+B_2^2+2A_2B_2\cos{(2ik_2x)}\\
&\hspace{0.25cm}+\left(\frac{1}{k_2^2}\right)k_2^2\left[A_2^2+B_2^2-2A_2B_2\cos{(2ik_2x)}\right]\\
&=2(A_2^2+B_2^2).
\end{align*}
To understand what the expressions in the previous hint tell you about the relationship between the wavenumber \(k\) and the amplitude of the wavefunction \(\psi(x)\), first note that the terms \(A_1^2+B_1^2\) and \(A_2^2+B_2^2\) represent the amplitude of the wavefunction on each side of the boundary (you can see proof of this in the next problem). If you call those amplitudes \(F_1\) and \(F_2\), the previous equations can be written as
\begin{equation*}
|\psi_1(x)|^2+\frac{1}{k_1^2}\bigg|\frac{\partial \psi_1(x)}{\partial x}\bigg|^2=F_1
\end{equation*}
and
\begin{align*}
|\psi_2(x)|^2+\frac{1}{k_2^2}\bigg|\frac{\partial \psi_2(x)}{\partial x}\bigg|^2=F_2.
\end{align*}
Now consider the terms on the left side of these equations. Since the wavefunction \(\psi(x)\) and its slope \(\partial \psi(x)/\partial x\) must be continuous across the boundary, the square magnitudes of these quantities must be the same a tiny distance to the left of the boundary and a tiny distance to the right of the boundary. But if those quantities are the same on opposite sides of the boundary, then the \(1/k_1^2\) and \(1/k_2^2\) terms mean that if \(1/k_1^2\) is larger than \(1/k_2^2\) (which means that \(k_1\) is smaller than \(k_2\)), them \(F_1\) must be larger than \(F_2\).
This means that the wavefunction on the side of the boundary with smaller wavenumber \(k\) has larger amplitude than the wavefunction on the side of the boundary with larger wavenumber.
As described in Section 4.3, both the wavefunction \(\psi(x)\) and its slope (the first spatial derivative) \(\partial \psi(x)/\partial x\) must be continuous across the boundary.
For the wavefunction with form
\begin{equation*}
\psi(x)=Ae^{ikx}+Be^{-ikx}
\end{equation*}
you can write the wavefunctions \(\psi_1(x)\) on one side of the boundary and \(\psi_2(x)\) on the other side of the boundary as
\begin{equation*}
\psi_1(x)=A_1e^{ik_1x}+B_1e^{-ik_1x}
\end{equation*}
and
\begin{equation*}
\psi_2(x)=A_2e^{ik_2x}+B_2e^{-ik_2x}
\end{equation*}
and their first spatial derivatives as
\begin{align*}
\frac{\partial \psi_1(x)}{\partial x}&=\frac{\partial (A_1e^{ik_1x})}{\partial x}+\frac{\partial (B_1e^{-ik_1x})}{\partial x}\\
&=ik_1A_1e^{ik_1x}-ik_1B_1e^{-ik_1x}
\end{align*}
and
\begin{align*}
\frac{\partial \psi_2(x)}{\partial x}&=\frac{\partial (A_2e^{ik_2x})}{\partial x}+\frac{\partial (B_2e^{-ik_2x})}{\partial x}\\
&=ik_2A_2e^{ik_2x}-ik_2B_2e^{-ik_2x}.
\end{align*}
To use the continuity of the wavefunction \(\psi\) and its derivative across the boundary to find the relationship between wavenumber and amplitude, find the square magnitude of each of these expressions. The squares of \(\psi\) and its spatial derivative on each side of the boundary are
\begin{align*}
|\psi_1(x)|^2=(\psi_1)(\psi_1)^*&=(A_1e^{ik_1x}+B_1e^{-ik_1x})(A_1e^{ik_1x}+B_1e^{-ik_1x})^*\\
&=A_1^2+B_1^2+A_1B_1\left(e^{2ik_1x}+e^{-2ik_1x}\right)\\
&=A_1^2+B_1^2+2A_1B_1\cos{(2ik_1x)}
\end{align*}
\begin{align*}
|\psi_2(x)|^2=(\psi_2)(\psi_2)^*&=(A_2e^{ik_2x}+B_2e^{-ik_2x})(A_2e^{ik_2x}+B_2e^{-ik_2x})^*\\
&=A_2^2+B_2^2+A_2B_2\left(e^{2ik_2x}+e^{-2ik_2x}\right)\\
&=A_2^2+B_2^2+2A_2B_2\cos{(2ik_2x)}
\end{align*}
\begin{align*}
\bigg|\frac{\partial \psi_1(x)}{\partial x}\bigg|^2&=(ik_1A_1e^{ik_1x}-ik_1B_1e^{-ik_1x})(ik_1A_1e^{ik_1x}-ik_1B_1e^{-ik_1x})^*\\
&=k_1^2\left[A_1^2+B_1^2-A_1B_1\left(e^{2ik_1x}+e^{-2ik_1x}\right)\right]\\
&=k_1^2\left[A_1^2+B_1^2-2A_1B_1\cos{(2ik_1x)}\right]
\end{align*}
\begin{align*}
\bigg|\frac{\partial \psi_2(x)}{\partial x}\bigg|^2&=(ik_2A_2e^{ik_2x}-ik_2B_2e^{-ik_2x})(ik_2A_2e^{ik_2x}-ik_2B_1e^{-ik_2x})^*\\
&=k_2^2\left[A_2^2+B_2^2-A_2B_2\left(e^{2ik_2x}+e^{-2ik_2x}\right)\right]\\
&=k_2^2\left[A_2^2+B_2^2-2A_2B_2\cos{(2ik_2x)}\right].
\end{align*}
In these expressions, the \(A_1^2+B_1^2\) and \(A_2^2+B_2^2\) provide information about the amplitude of the wavefunctions on opposite sides of the boundary, but those pesky \(2A_1B_1\cos{(2ik_1x)}\) and \(2A_2B_2\cos{(2ik_2x)}\) cross terms make it somewhat difficult to see that information.
Notice, however, that the cross terms in \(|\psi|^2\) have the opposite signs of those in \(|\frac{\partial \psi}{\partial x}|^2\). So those cross terms will cancel if you add \(|\psi|^2\) to \(|\frac{\partial \psi}{\partial x}|^2\) (after dividing the latter by the \(k^2\) factor that appears in \(|\frac{\partial \psi}{\partial x}|^2\) but not in \(|\psi|^2\)).
These additions give
\begin{align*}
|\psi_1(x)|^2+\frac{1}{k_1^2}\bigg|\frac{\partial \psi_1(x)}{\partial x}\bigg|^2&=A_1^2+B_1^2+2A_1B_1\cos{(2ik_1x)}\\
&\hspace{0.25cm}+\left(\frac{1}{k_1^2}\right)k_1^2\left[A_1^2+B_1^2-2A_1B_1\cos{(2ik_1x)}\right]\\
&=2(A_1^2+B_1^2)
\end{align*}
and
\begin{align*}
|\psi_2(x)|^2+\frac{1}{k_2^2}\bigg|\frac{\partial \psi_2(x)}{\partial x}\bigg|^2&=A_2^2+B_2^2+2A_2B_2\cos{(2ik_2x)}\\
&\hspace{0.25cm}+\left(\frac{1}{k_2^2}\right)k_2^2\left[A_2^2+B_2^2-2A_2B_2\cos{(2ik_2x)}\right]\\
&=2(A_2^2+B_2^2).
\end{align*}
To understand what these expressions tell you about the relationship between the wavenumber \(k\) and the amplitude of the wavefunction \(\psi(x)\), first note that the terms \(A_1^2+B_1^2\) and \(A_2^2+B_2^2\) represent the amplitude of the wavefunction on each side of the boundary (you can see proof of this in the next problem). If you call those amplitudes \(F_1\) and \(F_2\), these equations can be written as
\begin{equation*}
|\psi_1(x)|^2+\frac{1}{k_1^2}\bigg|\frac{\partial \psi_1(x)}{\partial x}\bigg|^2=F_1
\end{equation*}
and
\begin{align*}
|\psi_2(x)|^2+\frac{1}{k_2^2}\bigg|\frac{\partial \psi_2(x)}{\partial x}\bigg|^2=F_2.
\end{align*}
Now consider the terms on the left side of these equations. Since the wavefunction \(\psi(x)\) and its slope \(\partial \psi(x)/\partial x\) must be continuous across the boundary, the square magnitudes of these quantities must be the same a tiny distance to the left of the boundary and a tiny distance to the right of the boundary. But if those quantities are the same on opposite sides of the boundary, then the \(1/k_1^2\) and \(1/k_2^2\) terms mean that if \(1/k_1^2\) is larger than \(1/k_2^2\) (which means that \(k_1\) is smaller than \(k_2\)), them \(F_1\) must be larger than \(F_2\).
This means that the wavefunction on the side of the boundary with smaller wavenumber \(k\) has larger amplitude than the wavefunction on the side of the boundary with larger wavenumber.
Show that the expressions \(A_1\cos{(kx)}+B_1\sin{(kx)}\) and \(A_2\sin{(kx+\phi)}\) are equivalent to the expression \(Ae^{ikx}+Be^{-ikx}\), and find the relationship between the coefficients of these expressions.
To show the equivalence of the exponential expression \(Ae^{ikx}+Be^{-ikx}\) with the trigonometric expressions \(A_1\cos{(kx)}+B_1\sin{(kx)}\) and \(A_2\sin{(kx+\phi)}\), start by using the Euler relation
\begin{equation*}
e^{i\theta}=\cos{\theta}+i\sin{\theta}.
\end{equation*}
Applying the Euler relation to \(Ae^{ikx}+Be^{-ikx}\) gives
\begin{align*}
Ae^{ikx}+Be^{-ikx}&=A(\cos{(kx)}+i\sin{(kx)})+B(\cos{(kx)}-i\sin{(kx)})\\
&=(A+B)\cos{(kx)}+i(A-B)\sin{(kx)}
\end{align*}
which means that
\begin{equation*}
Ae^{ikx}+Be^{-ikx}=C\cos{(kx)}+D\sin{(kx)}
\end{equation*}
in which \(C=A+B\) and \(D=i(A-B)\).
To show that \(C\cos{(kx)}+D\sin{(kx)}\) is equivalent to \(F\sin{(kx+\phi)}\), use the trigonometric relation
\begin{equation*}
\sin{(x+y)}=\sin{x}\cos{y}+\cos{x}\sin{y}.
\end{equation*}
Applying the relation in the previous hint to the expression \(F\sin{(kx+\phi)}\) gives
\begin{equation*}
F\sin{(kx+\phi)}=F\sin{kx}\cos{\phi}+F\cos{kx}\sin{\phi}
\end{equation*}
which means that
\begin{equation*}
C\cos{(kx)}+D\sin{(kx)}=F\sin{(kx+\phi)}
\end{equation*}
in which \(C=F\sin{\phi}\) and \(D=F\cos{\phi}\).
To show the equivalence of the exponential expression \(Ae^{ikx}+Be^{-ikx}\) with the trigonometric expressions \(A_1\cos{(kx)}+B_1\sin{(kx)}\) and \(A_2\sin{(kx+\phi)}\), start by using the Euler relation
\begin{equation*}
e^{i\theta}=\cos{\theta}+i\sin{\theta}.
\end{equation*}
Applying the Euler relation to \(Ae^{ikx}+Be^{-ikx}\) gives
\begin{align*}
Ae^{ikx}+Be^{-ikx}&=A(\cos{(kx)}+i\sin{(kx)})+B(\cos{(kx)}-i\sin{(kx)})\\
&=(A+B)\cos{(kx)}+i(A-B)\sin{(kx)}
\end{align*}
which means that
\begin{equation*}
Ae^{ikx}+Be^{-ikx}=C\cos{(kx)}+D\sin{(kx)}
\end{equation*}
in which \(C=A+B\) and \(D=i(A-B)\).
To show that \(C\cos{(kx)}+D\sin{(kx)}\) is equivalent to \(F\sin{(kx+\phi)}\), use the trigonometric relation
\begin{equation*}
\sin{(x+y)}=\sin{x}\cos{y}+\cos{x}\sin{y}.
\end{equation*}
Applying this relation to the expression \(F\sin{(kx+\phi)}\) gives
\begin{equation*}
F\sin{(kx+\phi)}=F\sin{kx}\cos{\phi}+F\cos{kx}\sin{\phi}
\end{equation*}
which means that
\begin{equation*}
C\cos{(kx)}+D\sin{(kx)}=F\sin{(kx+\phi)}
\end{equation*}
in which \(C=F\sin{\phi}\) and \(D=F\cos{\phi}\).
Use L’Hôpital’s rule to find the value of the function \(\frac{\sin{\left(\frac{\Delta k}{2}x\right)}}{\frac{\Delta k}{2}x}\) at\(x=0\).
L’Hôpital’s rule says that
\begin{equation*}
\lim_{x \to 0} \frac{f(x)}{g(x)}=\lim_{x \to 0}\frac{f'(x)}{g'(x)}
\end{equation*}
in which \(f'(x)=\frac{df(x)}{dx}\) and \(g'(x)=\frac{dg(x)}{dx}\).
Applying L’Hôpital’s rule to find the value of the function \(\frac{\sin{\left(\frac{\Delta k}{2}x\right)}}{\frac{\Delta k}{2}x}\) at \(x=0\) gives
\begin{equation*}
\lim_{x \to 0} \frac{\sin{\left(\frac{\Delta k}{2}x\right)}}{\frac{\Delta k}{2}x}=\lim_{x \to 0}\frac{\frac{d\left[\sin{\left(\frac{\Delta k}{2}x\right)}\right]}{dx}}{\frac{d\left[\frac{\Delta k}{2}x\right]}{dx}}.
\end{equation*}
Carrying out the differentiation in the previous hint gives
\begin{align*}
\lim_{x \to 0} \frac{\sin{\left(\frac{\Delta k}{2}x\right)}}{\frac{\Delta k}{2}x}&=\lim_{x \to 0}\frac{\frac{\Delta k}{2}\cos{\left(\frac{\Delta k}{2}x\right)}}{\frac{\Delta k}{2}}\\
&=\frac{\frac{\Delta k}{2}\cos{\left(0\right)}}{\frac{\Delta k}{2}}=1.
\end{align*}
Full Solution: L’Hôpital’s rule says that
\begin{equation*}
\lim_{x \to 0} \frac{f(x)}{g(x)}=\lim_{x \to 0}\frac{f'(x)}{g'(x)}
\end{equation*}
in which \(f'(x)=\frac{df(x)}{dx}\) and \(g'(x)=\frac{dg(x)}{dx}\).
Applying L’Hôpital’s rule to find the value of the function \(\frac{\sin{\left(\frac{\Delta k}{2}x\right)}}{\frac{\Delta k}{2}x}\) at\(x=0\) gives
\begin{equation*}
\lim_{x \to 0} \frac{\sin{\left(\frac{\Delta k}{2}x\right)}}{\frac{\Delta k}{2}x}=\lim_{x \to 0}\frac{\frac{d\left[\sin{\left(\frac{\Delta k}{2}x\right)}\right]}{dx}}{\frac{d\left[\frac{\Delta k}{2}x\right]}{dx}}.
\end{equation*}
Carrying out this differentiation gives
\begin{align*}
\lim_{x \to 0} \frac{\sin{\left(\frac{\Delta k}{2}x\right)}}{\frac{\Delta k}{2}x}&=\lim_{x \to 0}\frac{\frac{\Delta k}{2}\cos{\left(\frac{\Delta k}{2}x\right)}}{\frac{\Delta k}{2}}\\
&=\frac{\frac{\Delta k}{2}\cos{\left(0\right)}}{\frac{\Delta k}{2}}=1.
\end{align*}
Show that plugging the expression for \(\phi(k)\) from the Fourier transform (Eq. 4.14) into the inverse Fourier transform (Eq. 4.15) leads to the Dirac delta-function expression given in Eq. 4.34.
Eq. 4.14 for \(\phi(k)\) is
\begin{equation*}
\phi(k)=\frac{1}{\sqrt{2\pi}}\int_{-\infty}^\infty \psi(x)e^{-ikx}dx
\end{equation*}
and Eq. 4.15 for \(\psi(x)\) is
need is the inverse Fourier transform\index{inverse Fourier tranform}
\begin{equation*}
\psi(x)=\frac{1}{\sqrt{2\pi}}\int_{-\infty}^\infty \phi(k)e^{ikx}dk,
\end{equation*}
so plugging the expression for \(\phi(k)\) into the expression for \(\psi(x)\) looks like this:
\begin{equation*}
\psi(x)=\frac{1}{\sqrt{2\pi}}\int_{-\infty}^\infty \frac{1}{\sqrt{2\pi}}\left[\int_{-\infty}^\infty \psi(x’)e^{-ikx’}dx’\right]e^{ikx}dk
\end{equation*}
in which the variable of integration has been written as \(x’\) in the inner integral in order to differentiate that variable from the variable\(x\) in the outer integral.
Moving the \(e^{ikx}\) factor inside the \(dx’\) integral makes the expression in the previous hint
\begin{align*}
\psi(x)&=\frac{1}{\sqrt{2\pi}}\int_{-\infty}^\infty \frac{1}{\sqrt{2\pi}}\left[\int_{-\infty}^\infty \psi(x’)e^{-ikx’}e^{ikx}dx’\right]dk\\
&=\frac{1}{\sqrt{2\pi}}\int_{-\infty}^\infty \frac{1}{\sqrt{2\pi}}\left[\int_{-\infty}^\infty \psi(x’)e^{ik(x-x’)}dx’\right]dk.
\end{align*}
Combining the multiplicative constants and interchanging the order of integration (which you’re allowed to do as long as the integral converges) makes the expression from the previous hint
\begin{align*}
\psi(x)&=\frac{1}{2\pi}\int_{-\infty}^\infty \left[\int_{-\infty}^\infty \psi(x’)e^{ik(x-x’)}dk\right]dx’\\
&=\frac{1}{2\pi}\int_{-\infty}^\infty\psi(x’) \left[\int_{-\infty}^\infty e^{ik(x-x’)}dk\right]dx’.
\end{align*}
Recall the sifting properties of the Dirac delta function (Eq. 4.31):
\begin{equation*}
f(x)=\int_{-\infty}^\infty f(x’)\delta(x’-x)dx’.
\end{equation*}
Comparing this equation to the expression for \(\psi(x)\) in the previous hint means
\begin{equation*}
\frac{1}{\sqrt{2\pi}}\int_{-\infty}^\infty e^{ik(x-x’)}dk=\delta(x’-x)=\delta(x-x’)
\end{equation*}
in agreement with Eq. 4.34.
Eq. 4.14 for \(\phi(k)\) is
\begin{equation*}
\phi(k)=\frac{1}{\sqrt{2\pi}}\int_{-\infty}^\infty \psi(x)e^{-ikx}dx
\end{equation*}
and Eq. 4.15 for \(\psi(x)\) is
need is the inverse Fourier transform\index{inverse Fourier tranform}
\begin{equation*}
\psi(x)=\frac{1}{\sqrt{2\pi}}\int_{-\infty}^\infty \phi(k)e^{ikx}dk,
\end{equation*}
so plugging the expression for \(\phi(k)\) into the expression for \(\psi(x)\) looks like this:
\begin{equation*}
\psi(x)=\frac{1}{\sqrt{2\pi}}\int_{-\infty}^\infty \frac{1}{\sqrt{2\pi}}\left[\int_{-\infty}^\infty \psi(x’)e^{-ikx’}dx’\right]e^{ikx}dk
\end{equation*}
in which the variable of integration has been written as \(x’\) in the inner integral in order to differentiate that variable from the variable \(x\) in the outer integral.
Moving the \(e^{ikx}\) factor inside the \(dx’\) integral makes this expression
\begin{align*}
\psi(x)&=\frac{1}{\sqrt{2\pi}}\int_{-\infty}^\infty \frac{1}{\sqrt{2\pi}}\left[\int_{-\infty}^\infty \psi(x’)e^{-ikx’}e^{ikx}dx’\right]dk\\
&=\frac{1}{\sqrt{2\pi}}\int_{-\infty}^\infty \frac{1}{\sqrt{2\pi}}\left[\int_{-\infty}^\infty \psi(x’)e^{ik(x-x’)}dx’\right]dk.
\end{align*}
Combining the multiplicative constants and interchanging the order of integration makes this expression
\begin{align*}
\psi(x)&=\frac{1}{2\pi}\int_{-\infty}^\infty \left[\int_{-\infty}^\infty \psi(x’)e^{ik(x-x’)}dk\right]dx’\\
&=\frac{1}{2\pi}\int_{-\infty}^\infty\psi(x’) \left[\int_{-\infty}^\infty e^{ik(x-x’)}dk\right]dx’.
\end{align*}
Recall the sifting properties of the Dirac delta function (Eq. 4.31):
\begin{equation*}
f(x)=\int_{-\infty}^\infty f(x’)\delta(x’-x)dx’.
\end{equation*}
Comparing this equation to the expression for \(\psi(x)\) means
\begin{equation*}
\frac{1}{\sqrt{2\pi}}\int_{-\infty}^\infty e^{ik(x-x’)}dk=\delta(x’-x)=\delta(x-x’)
\end{equation*}
in agreement with Eq. 4.34.
Derive the momentum-space representation of the position eigenfunctions \(\tilde{\phi}(p)\) (Eq. 4.65) and the position operator \(\widehat{X}\) (Eq. 4.66).
To find the momentum-space representation of the position eigenfunctions, start by recalling from Eq. 4.38 that the momentum wavefunction \(\tilde{\phi}(p)\) is the Fourier transform of the position wavefunction \(\psi(x)\):
\begin{equation*}
\tilde{\phi}(p)=\frac{1}{\sqrt{2\pi}}\int_{-\infty}^\infty \psi(x)e^{-i\frac{p}{\hbar}x}dx.
\end{equation*}
Recall also that the position eigenfunctions in position space are Dirac delta functions of position \(\delta(x-x’)\).
Plugging the position delta functions \(\delta(x-x’)\) into the equation for \(\tilde{\phi}(p)\) given in the previous hint leads to
\begin{equation*}
\tilde{\phi}(p)=\frac{1}{\sqrt{2\pi}}\int_{-\infty}^\infty \delta(x-x’)e^{-i\frac{p}{\hbar}x}dx,
\end{equation*}
and the sifting property of the delta function makes this
\begin{equation*}
\tilde{\phi}(p)=\frac{1}{\sqrt{2\pi}}e^{-i\frac{p}{\hbar}x’}
\end{equation*}
and since the variable name \(x’\) is arbitrary, you can rename it \(x\), making the position eigenfunctions in momentum space
\begin{equation*}
\tilde{\phi}_x(p)=\frac{1}{\sqrt{2\pi}}e^{-i\frac{p}{\hbar}x}.
\end{equation*}
in agreement with Eq. 4.65.
To find momentum-space representation of the position operator \(\widehat{X}_p\), begin by writing the eigenvalue equation for the position operator in \(\widehat{X}_p\) operating on the position eigenfunctions \(\tilde{\phi}_x(p)\) in momentum space:
\begin{equation*}
\widehat{X}_p\tilde{\phi}_x(p)=x\tilde{\phi}_x(p).
\end{equation*}
Plugging in the expression for the momentum-space representation of the position eigenfunctions \(\tilde{\phi}_x(p)\) from Part (a) of this problem yields
\begin{equation*}
\widehat{X}_p\left(\frac{1}{\sqrt{2\pi}}e^{-i\frac{p}{\hbar}x}\right)=x\left(\frac{1}{\sqrt{2\pi}}e^{-i\frac{p}{\hbar}x}\right).
\end{equation*}
To determine the mathematical form of the position operator in momentum space, apply the same logic as used in Section 4.5 to the eigenvalue equation in the previous hint.
Specifically, ask yourself what kind of operation can pull a factor of \(x\) out of the function \(\frac{1}{\sqrt{2\pi}}e^{-i\frac{p}{\hbar}x}\).
If your answer to the question posed in the previous hint was “Taking the derivative with respect to \(p\) pulls a factor of \(x\) out of the function \(\frac{1}{\sqrt{2\pi}}e^{-i\frac{p}{\hbar}x}\)”, you’re correct. So the position operator in momentum space definitely involves the operation \(\partial/\partial p\).
Note, however, that
\begin{equation*}
\frac{\partial \left(\frac{1}{\sqrt{2\pi}}e^{-i\frac{p}{\hbar}x}\right)}{\partial p}=\left(-i\frac{x}{\hbar}\right)\left(\frac{1}{\sqrt{2\pi}}e^{-i\frac{p}{\hbar}x}\right),
\end{equation*}
so in addition to pulling out a factor of \(x\), taking the derivative with respect to\(p\) also brings down the constant factor \(-\frac{i}{\hbar}\).
To cancel those unwanted factors, multiply the partial derivative by \(-\frac{\hbar}{i}=i\hbar\):
\begin{equation*}
i\hbar \frac{\partial \left(\frac{1}{\sqrt{2\pi}}e^{-i\frac{p}{\hbar}x}\right)}{\partial p}=x\left(\frac{1}{\sqrt{2\pi}}e^{-i\frac{p}{\hbar}x}\right),
\end{equation*}
which means that the position operator \(\widehat{X}_p\) in momentum space can be represented as
\begin{equation*}
\widehat{X}_p=i\hbar \frac{\partial}{\partial p}.
\end{equation*}
Part (a):
To find the momentum-space representation of the position eigenfunctions, start by recalling from Eq. 4.38 that the momentum wavefunction \(\tilde{\phi}(p)\) is the Fourier transform of the position wavefunction \(\psi(x)\):
\begin{equation*}
\tilde{\phi}(p)=\frac{1}{\sqrt{2\pi}}\int_{-\infty}^\infty \psi(x)e^{-i\frac{p}{\hbar}x}dx.
\end{equation*}
Recall also that the position eigenfunctions in position space are Dirac delta functions of position \(\delta(x-x’)\).
Plugging the position delta functions \(\delta(x-x’)\) into this equation for \(\tilde{\phi}(p)\) gives
\begin{equation*}
\tilde{\phi}(p)=\frac{1}{\sqrt{2\pi}}\int_{-\infty}^\infty \delta(x-x’)e^{-i\frac{p}{\hbar}x}dx,
\end{equation*}
and the sifting property of the delta function makes this
\begin{equation*}
\tilde{\phi}(p)=\frac{1}{\sqrt{2\pi}}e^{-i\frac{p}{\hbar}x’}.
\end{equation*}
Since the variable name \(x’\) is arbitrary, you can rename it \(x\), making the position eigenfunctions in momentum space
\begin{equation*}
\tilde{\phi}_x(p)=\frac{1}{\sqrt{2\pi}}e^{-i\frac{p}{\hbar}x}.
\end{equation*}
in agreement with Eq. 4.65.
Part (b):
To find momentum-space representation of the position operator \(\widehat{X}_p\), begin by writing the eigenvalue equation for the position operator in \(\widehat{X}_p\) operating on the position eigenfunctions\(\tilde{\phi}_x(p)\) in momentum space:
\begin{equation*}
\widehat{X}_p\tilde{\phi}_x(p)=x\tilde{\phi}_x(p).
\end{equation*}
Plugging in the expression for the momentum-space representation of the position eigenfunctions \(\tilde{\phi}_x(p)\) from Part (a) of this problem yields
\begin{equation*}
\widehat{X}_p\left(\frac{1}{\sqrt{2\pi}}e^{-i\frac{p}{\hbar}x}\right)=x\left(\frac{1}{\sqrt{2\pi}}e^{-i\frac{p}{\hbar}x}\right).
\end{equation*}
To determine the mathematical form of the position operator in momentum space, apply the same logic as used in Section 4.5 to the eigenvalue equation. Specifically, ask yourself what kind of operation can pull a factor of \(x\) out of the function \(\frac{1}{\sqrt{2\pi}}e^{-i\frac{p}{\hbar}x}\).
If your answer to this question was “Taking the derivative with respect to\(p\) pulls a factor of \(x\) out of the function \(\frac{1}{\sqrt{2\pi}}e^{-i\frac{p}{\hbar}x}\)”, you’re correct. So the position operator in momentum space definitely involves the operation \(\partial/\partial p\).
Note, however, that
\begin{equation*}
\frac{\partial \left(\frac{1}{\sqrt{2\pi}}e^{-i\frac{p}{\hbar}x}\right)}{\partial p}=\left(-i\frac{x}{\hbar}\right)\left(\frac{1}{\sqrt{2\pi}}e^{-i\frac{p}{\hbar}x}\right),
\end{equation*}
so in addition to pulling out a factor of \(x\), taking the derivative with respect to \(p\) also brings down the constant factor \(-\frac{i}{\hbar}\).
To cancel those unwanted factors, multiply the partial derivative by \(-\frac{\hbar}{i}=i\hbar\):
\begin{equation*}
i\hbar \frac{\partial \left(\frac{1}{\sqrt{2\pi}}e^{-i\frac{p}{\hbar}x}\right)}{\partial p}=x\left(\frac{1}{\sqrt{2\pi}}e^{-i\frac{p}{\hbar}x}\right),
\end{equation*}
which means that the position operator \(\widehat{X}_p\) in momentum space can be represented as
\begin{equation*}
\widehat{X}_p=i\hbar \frac{\partial}{\partial p}.
\end{equation*}
Use the momentum-space representations of the position and momentum operators to find the commutator \([\widehat{X},\widehat{P}]\).
The commutator \([\widehat{X}, \widehat{P}]\) is defined as
\begin{equation*}
[\widehat{X},\widehat{P}]=\widehat{X}\widehat{P}-\widehat{P}\widehat{X}
\end{equation*}
and the momentum-space representations of the position operator \(\widehat{X}_p\) and the momentum operator \(\widehat{P}\) are
\begin{equation*}
\widehat{X}_p=i\hbar\frac{\partial}{\partial p}
\end{equation*}
and
\begin{equation*}
\widehat{P}=p.
\end{equation*}
Plugging the momentum-space representations of the position and momentum operators into the commutator equation gives
\begin{equation*}
[\widehat{X}_p,\widehat{P}]=\widehat{X}_p\widehat{P}-\widehat{P}\widehat{X}_p=\left(i\hbar\frac{\partial}{\partial p}\right)(p)-(p)\left(i\hbar\frac{\partial}{\partial p}\right).
\end{equation*}
To analyze this commutator, remember the admonition in the text to always provide a function on which the operators can operate.
The commutator \([\widehat{X}_p,\widehat{P}]\) operating on function \(\phi\) looks like this:
\begin{equation*}
[\widehat{X}_p,\widehat{P}]\phi=\left[\left(i\hbar\frac{\partial}{\partial p}\right)(p)\right]\phi-\left[(p)\left(i\hbar\frac{\partial}{\partial p}\right)\right]\phi.
\end{equation*}
Performing the operations on \(\phi\) by the commutator \([\widehat{X}_p, \widehat{P}]\) gives:
\begin{align*}
[\widehat{X}_p,\widehat{P}]\phi&=i\hbar\frac{\partial (p\phi)}{\partial p}-i\hbar p\frac{\partial\phi}{\partial p}\\
&=i\hbar\phi+i\hbar p \frac{\partial \phi}{\partial p}-i\hbar p\frac{\partial\phi}{\partial p}\\
&=i\hbar\phi
\end{align*}
and now that the function \(\phi\) has done its job, you can remove it and write the commutator as
\begin{equation*}
[\widehat{X}_p,\widehat{P}]=i\hbar.
\end{equation*}
The commutator \([\widehat{X}, \widehat{P}]\) is defined as
\begin{equation*}
[\widehat{X},\widehat{P}]=\widehat{X}\widehat{P}-\widehat{P}\widehat{X}
\end{equation*}
and the momentum-space representations of the position operator \(\widehat{X}_p\) and the momentum operator \(\widehat{P}\) are
\begin{equation*}
\widehat{X}_p=i\hbar\frac{\partial}{\partial p}
\end{equation*}
and
\begin{equation*}
\widehat{P}=p.
\end{equation*}
Plugging the momentum-space representations of the position and momentum operators into the commutator equation gives
\begin{equation*}
[\widehat{X}_p,\widehat{P}]=\widehat{X}_p\widehat{P}-\widehat{P}\widehat{X}_p=\left(i\hbar\frac{\partial}{\partial p}\right)(p)-(p)\left(i\hbar\frac{\partial}{\partial p}\right).
\end{equation*}
To analyze this commutator, remember the admonition in the text to always provide a function on which the operators can operate. The commutator \([\widehat{X}_p, \widehat{P}]\) operating on function \(\phi\) looks like this:
\begin{equation*}
[\widehat{X}_p,\widehat{P}]\phi=\left[\left(i\hbar\frac{\partial}{\partial p}\right)(p)\right]\phi-\left[(p)\left(i\hbar\frac{\partial}{\partial p}\right)\right]\phi,
\end{equation*}
and performing the operations on \(\phi\) by the commutator \([\widehat{X}_p,\widehat{P}]\) gives:
\begin{align*}
[\widehat{X}_p,\widehat{P}]\phi&=i\hbar\frac{\partial (p\phi)}{\partial p}-i\hbar p\frac{\partial\phi}{\partial p}\\
&=i\hbar\phi+i\hbar p \frac{\partial \phi}{\partial p}-i\hbar p\frac{\partial\phi}{\partial p}\\
&=i\hbar\phi.
\end{align*}
Now that the function \(\phi\) has done its job, you can remove it and write the commutator as
\begin{equation*}
[\widehat{X}_p,\widehat{P}]=i\hbar.
\end{equation*}
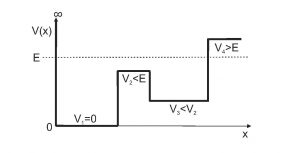
For piecewise-constant potentials such as this, consider the relative value of the energy \(E\) and the potential \(V\) in each region. To do that, it’s helpful to label each region, like this:
In Region 1, the potential is infinite, which means that this is a classically disallowed region, so the wavefunction decays exponentially. And since the potential \(V\) in this region is infinitely larger than energy \(E\), that exponential decay is infinitely fast (over distance), so the wavefunction does not exist in Region 1.
In Region 1, the potential is infinite, which means that this is a classically disallowed region, so the wavefunction decays exponentially. And since the potential \(V\) in this region is infinitely larger than energy \(E\), that exponential decay is infinitely fast (over distance), so the wavefunction does not exist in Region 1.
In Region 2, \(E>V\), so this is a classically allowed region, and the difference between \(E\) and \(V\) is larger than in any of the other classically allowed regions. As described in Section 4.3, larger \(E-V\) means shorter wavelength and smaller amplitude than in other regions.
Region 3 also has \(E>V\), so this is also a classically allowed region, but in this region the difference between \(E\) and \(V\) is smaller than in any other of the classically allowed regions. That means that the wavelength must be shorter and the amplitude must be larger than in other regions.
As in Regions 2 and 3, in Region 4 \(E>V\), so this is also a classically allowed region. Since the difference between \(E\) and \(V\) in this region is intermediate between the differences in Regions 2 and 3, the wavelength and amplitude in this region must be intermediate between the wavelengths and amplitudes in Regions 2 and 3.
In Region 5, \(V>E\), so like Region 1, Region 5 is classically disallowed. However, in this region the difference between \(E\) and \(V\) is finite, which means that the wavefunction will decay exponentially at a finite rate.
To sketch the wavefunction, use the characteristics described in previous hints:
Region 1: No wavefunction
Region 2: Oscillating, short \(\lambda\), small amplitude
Region 3: Oscillating, long \(\lambda\), large amplitude
Region 4: Oscillating, intermediate \(\lambda\) and amplitude
Region 5: Exponentially decaying at finite rate
and remember that the wavefunction amplitude and slope must be continuous across each boundary.
Your wavefunction might look something like this:
For piecewise-constant potentials such as this, consider the relative value of the energy \(E\) and the potential \(V\) in each region. To do that, it’s helpful to label each region, like this:
In Region 1, the potential is infinite, which means that this is a classically disallowed region, so the wavefunction decays exponentially. And since the potential \(V\) in this region is infinitely larger than energy \(E\), that exponential decay is infinitely fast (over distance), so the wavefunction does not exist in Region 1.
In Region 2, \(E>V\), so this is a classically allowed region, and the difference between \(E\) and \(V\) is larger than in any of the other classically allowed regions. As described in Section 4.3, larger \(E-V\) means shorter wavelength and smaller amplitude than in other regions.
Region 3 also has \(E>V\), so this is also a classically allowed region, but in this region the difference between \(E\) and \(V\) is smaller than in any other of the classically allowed regions. That means that the wavelength must be shorter and the amplitude must be larger than in other regions.
As in Regions 2 and 3, in Region 4 \(E>V\), so this is also a classically allowed region. Since the difference between \(E\) and \(V\) in this region is intermediate between the differences in Regions 2 and 3, the wavelength and amplitude in this region must be intermediate between the wavelengths and amplitudes in Regions 2 and 3.
In Region 5, \(V>E\), so like Region 1, Region 5 is classically disallowed. However, in this region the difference between \(E\) and \(V\) is finite, which means that the wavefunction will decay exponentially at a finite rate.
To sketch the wavefunction, use the characteristics described above:
Region 1: No wavefunction
Region 2: Oscillating, short \(\lambda\), small amplitude
Region 3: Oscillating, long \(\lambda\), large amplitude
Region 4: Oscillating, intermediate \(\lambda\) and amplitude
Region 5: Exponentially decaying at finite rate
and remember that the wavefunction amplitude and slope must be continuous across each boundary.
Your wavefunction might look something like this:
After working through this chapter, readers will be able to describe the Born rule and the Copenhagen interpretation of quantum mechanics, explain the relationship between quantum states and wavefunctions, delineate the required characteristics of quantum wavefunctions, and use Fourier theory to synthesize quantum wave packets and to relate position-space and momentum-space wavefunctions and operators.
Use the Born rule to relate the square magnitude of the wavefunction to probability density
Explain the tenets of the Copenhagen interpretation
Describe a quantum wavefunction as the amount of each eigenfunction in a quantum state
Determine a quantum wavefunction by projecting a quantum state onto a set of basis functions
Explain the difference between making a quantum measurement and applying an operator to a state
Explain why quantum wavefunctions must be smooth, single-valued, and square-integrable
Relate a wavefunction’s curvature to the energy in the region
Describe the behavior of wavefunctions in classically allowed and unallowed regions
Explain Fourier transforms using the multiplication of sinusoids and rotating phasors
Relate the width of a position wavefunction to the width of the corresponding momentum wavefunction
Apply the Heisenberg Uncertainty principle to incompatible observables
Relate position-space and momentum-space wavefunctions and operators using the Fourier transform
Explain how the canonical commutation relation affects measurements of quantum observables